递归算法
在函数或子过程的内部,直接或者间接地调用自己的算法。
特点:
- (1) 递归就是在过程或函数里调用自身。
- (2) 在使用递归策略时,必须有一个明确的递归结束条件,称为递归出口。
- (3) 递归算法解题通常显得很简洁,但递归算法解题的运行效率较低。所以一般不提倡用递归算法设计程序。
- (4) 在 递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成 栈溢出等。所以一般不提倡用递归算法设计程序。
递归算法一般用于解决三类问题:
- (1)数据的定义是按递归定义的。(Fibonacci函数)
- (2)问题解法按递归算法实现。(回溯)
- (3)数据的结构形式是按递归定义的。(树的遍历,图的搜索)
递归设计经验:
- 找重复(子问题)
- 找重复中的变化量–>参数
- 找参数变化趋势 –> 设计出口
解递归的常见思路:
- 切蛋糕思维,如求阶乘f(n) = n * f(n-1),数组就和,翻转字符串。
- 化不开的,看有没有递推公式?有没有等价转化? 如:斐波那契数列f(n) = f(n-1) + f(n-2),求最大公约数:f(m,n) = f(n, m%n)。
递归算法C语言实例
利用递归实现1到100以内的求和;
1 |
|
利用递归求阶乘:
1 |
|
利用递归求数组中最大数:
1 |
|
递归算法java语言实例:
斐波那契序列:
斐波那契数列问题,等价于两个子问题:
- 求前一项
- 求前两项
- 两项求和
1 | public class 斐波那契序列 { |
运行结果:
1 | 1 1 2 3 5 8 13 21 34 |
最大公约数:
1 | public class 最大公约数 { |
程序运行结果:
1 | 6 |
插入排序改递归:
1 | public class 递归_插入排序 { |
程序运行结果:
1 | 0 2 3 4 6 9 18 |
汉诺塔问题:
将1-N从A移动到B,C作为辅助。等价于:
- 1~N-1移动到C,A作为源,B作为辅助
- 把N从A移动到B
- 把1~N-1 从C移动到B,A为辅助
1 | public class 汉诺塔 { |
程序运行结果:
1 | 1: A-->B |
二分查找递归解法:
全范围二分查找,等价于三个子问题:
- 左边找(递归)
- 中间比
- 右边找(递归)
注意:左边查找和右边查找只选其一
1 | public class 递归_二分查找 { |
程序运行结果:
1 | 3 |
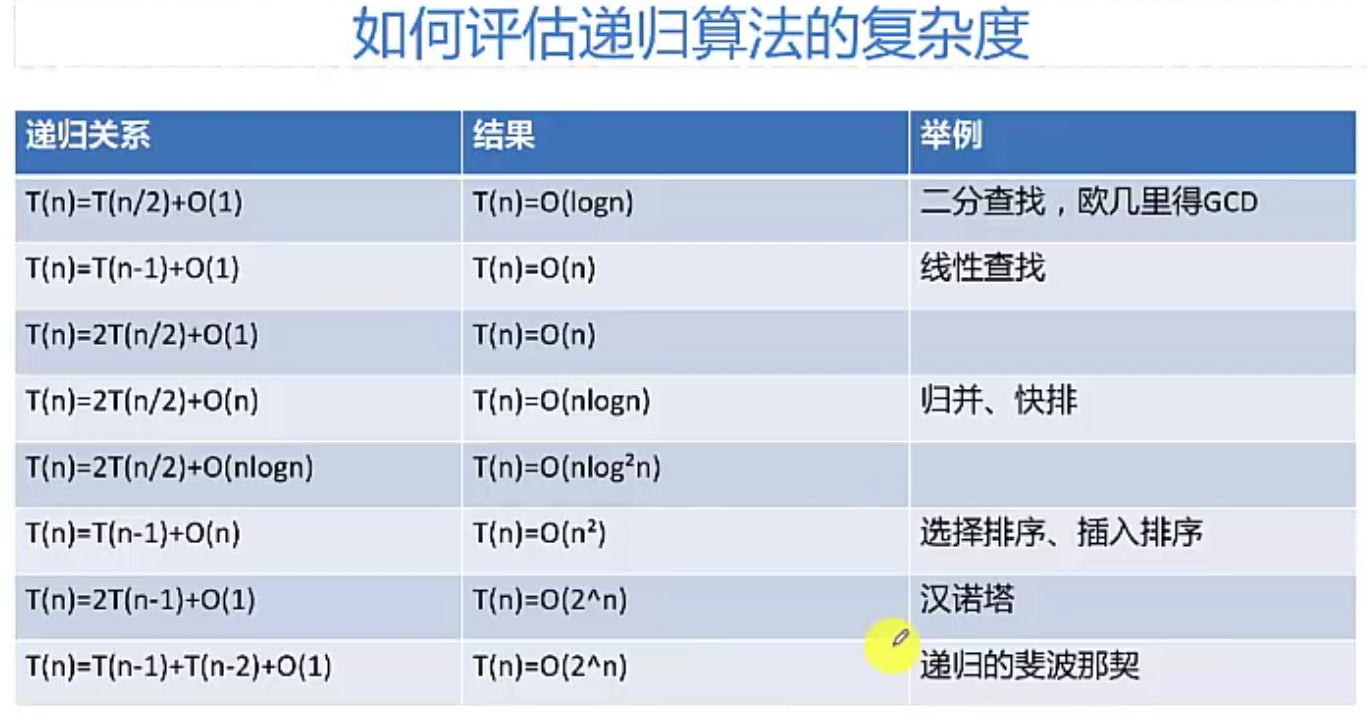
递归算法的性能分析:
斐波那契数列递归实现改进:
通过记录每次f(n)的值来防止大量重复计算,大大增加了性能。
1 | public static int fib(int n, int[] tmp) { |
改进前和改进后性能对比:
1 | public class 斐波那契序列 { |
程序运行结果:
1 | 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 |
小白上楼梯:
小白正在上楼梯,楼梯有n阶台阶,小白一次可以上1阶,2阶或者3阶,实现一个方法,计算小白有多少种走完楼梯的方式。
1 | public class 小白上楼梯 { |
程序运行结果:
1 | 1 2 4 7 13 24 44 81 149 274 504 927 1705 3136 5768 10609 19513 35890 66012 121415 223317 410744 755476 1389537 2555757 4700770 8646064 15902591 29249425 |
机器人走格子:
有一个X*Y的网格,一个机器人智能走格点且智能向右或向下走,要从左上角走到有下角。
请设计一个算法,计算机器人有多少种走法。
给定两个正整数int x,int y,请返回机器人的走法数目。保证x+y<=12.
1 | public class 机器人走方格 { |
程序运行结果:
1 | 70 |
合法括号:
实现一种算法,打印n对括号的全部有效组和(即左右括号正确配对)。
示例:
输入:3
输出:()()(), (()()), ()(()), (())(), ((()))
1 | import java.util.HashSet; |
程序运行结果:
1 | [()()(), (()()), ()(()), (())(), ((()))] |
硬币的表示:
假设我们有8种不同面值的硬币{1,2,5,10,20,50,100,200},用这些硬币组合构成一个给定的数值n。
例如n=200,那么一种可能的组合方式为 200 = 3 1 + 1*2 + 1*5 + 2*20 + 1 50 + 1 * 100.
问总共有多少种可能的组合方式? (这道题目来自著名编程网站ProjectEuler) 类似的题目还有:
[华为面试题] 1分2分5分的硬币三种,组合成1角,共有多少种组合
1x + 2y + 5*z=10
[创新工厂笔试题] 有1分,2分,5分,10分四种硬币,每种硬币数量无限,给定n分钱,有多少组合可以组成n分钱1 5 10 25 分 n,多少种组合方法.
1 | public class 硬币的表示 { |
程序执行结果:
1 | 4 |
非空子集生成之二进制法:
请编写一个方法,返回某集合的所有非空子集。
给定一个int数组A和数组的大小int n,请返回A的所有非空子集。
保证A的元素个数小于等于20,且元素互异。各子集内部从大到小排序,子集之间字典逆序排序
java示例代码:
1 | import java.util.ArrayList; |
程序运行结果:
1 | [[C, B, A], [C, B], [C, A], [C], [B, A], [B], [A]] |
全排列:
编写一个方法,确定某字符串的所有排列组合。
给定一个string A和一个int n,代表字符串和其长度,请返回所有该字符串字符的排列,
保证字符串长度小于等于11且字符串中字符均为大写英文字符,
解题思路:
以下实现了三种解法:
- 迭代法
- 交换法,回溯法
- 前缀法
java代码示例:
1 | import java.util.ArrayList; |
程序执行结果
1 | [CBA, BAC, BCA, CAB, ABC, ACB] |