二叉树的基本操作

发表于 | 更新于 | 分类于 | 阅读次数： | 字数： 1,660 | 阅读时长： 8

二叉树：

二叉树是树的特殊一种，具有如下特点：1、每个结点最多有两颗子树，结点的度最大为2。2、左子树和右子树是有顺序的，次序不能颠倒。3、即使某结点只有一个子树，也要区分左右子树。

满二叉树：

在一棵二叉树中，如果所有分支结点都有左孩子和右孩子结点，并且叶子结点都集中在二叉树的最下层，这样的树叫做满二叉树

完全二叉树：

若二叉树中最多只有最下面两层的结点的度数可以小于2，并且最下面一层的叶子结点都是依次排列在该层最左边的位置上，则称为完全二叉树

区别：

满二叉树是完全二叉树的特例，因为满二叉树已经满了，而完全并不代表满。所以形态你也应该想象出来了吧，满指的是出了叶子节点外每个节点都有两个孩子，而完全的含义则是最后一层没有满。

二叉树的五个重要性质：

  1. 在二叉树的第i层上最多有2 i-1 个节点 。（i>=1）
  2. 二叉树中如果深度为k,那么最多有2k-1个节点。(k>=1）
  3. n0=n2+1 n0表示度数为0的节点 n2表示度数为2的节点
  4. 在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]+1是向下取整。
  5. 若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点：
  1. 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点;
  2. 若 2i>n，则该结点无左孩子， 否则，编号为 2i 的结点为其左孩子结点；
  3. 2i+1>n，则该结点无右孩子结点， 否则，编号为2i+1 的结点为其右孩子结点。

二叉树的基本操作：

base.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//base.h
//-----公用的常量和类型----------

#include<iostream>
#include<stdlib.h>
#include<malloc.h>

using namespace std;

//函数结果状态码

#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define OVERFLOW -2

typedef int Status;
typedef char TElemType;

biTree.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
//biTree.h
//-----二叉树的基本函数实现------

//---------二叉树的链式存储表示------
typedef struct BiTNode{  //二叉树链表节点
    TElemType  date;  //数据域
    struct BiTNode *lchild, *rchild;  //左右孩子指针
}BiTNode, *BiTree;

//-----基本操作的函数原型说明------------

//构造空二叉树
Status InitBiTree(BiTree &T){
    if(!(T = (BiTNode *)malloc(sizeof(BiTNode))))//开辟节点空间
            exit(OVERFLOW);
    T == NULL;
    return OK;
}

//按先序次序输入二叉树中节点的值（一个字符），@字符表示空树
//构造二叉链表表示的二叉树T
Status CreateBiTree(BiTree &T){
    char ch;
    cin>>ch; //输入字符
    if(ch == '@') //判断输入的是否为@
        T = NULL;  //如果是@，T为空树
    else{
        if(!(T = (BiTNode *)malloc(sizeof(BiTNode))))//开辟节点空间
            exit(OVERFLOW);
        T->date = ch; //生成根节点
        CreateBiTree(T->lchild); //构造左子树
        CreateBiTree(T->rchild); //构造右子树
    }
    return OK;
}//CreateBitree

//销毁二叉树
Status DestroyBiTree(BiTree &T){
    if(T){
        DestroyBiTree(T->lchild);
        DestroyBiTree(T->rchild);
        free(T);
        T = NULL;
    }
    return OK;
}//DestroyBiTree

//判空
Status BiTreeEmpty(BiTree T){
    if(T)
        return FALSE;
    else
        return TRUE;
}//BiTreeEmpty

//递归求树的深度
int BiTreeDepth(BiTree T){
    int ldepth; //用来存放左子树的深度
    int rdepth; //右子树的深度
    if(!T) //树空
        return 0;
    ldepth = BiTreeDepth(T->lchild); //求左子树的深度
    rdepth = BiTreeDepth(T->rchild); //求右子树的深度
    return (ldepth > rdepth) ? (ldepth+1):(rdepth+1);
}//BiTreeDepth

//递归求叶子的个数
int BiTreeLeafCount(BiTree T){
    if(T == NULL)
        return 0;
    if(T->lchild == NULL && T->rchild == NULL)
        return 1;
    return BiTreeLeafCount(T->lchild) + BiTreeLeafCount(T->rchild);
}//BiTreeLeafCount

//求二叉树中节点个数
int NodeCount(BiTree T){
    if(T == NULL)
        return 0;
    return NodeCount(T->lchild) + NodeCount(T->rchild) + 1;
}//NodeCount

//求二叉树第K层的节点个数
int GetLevelNums(BiTree T, int k){
    if(T==NULL || k==0)
        return 0;
    if(k == 1)
        return 1;
    //左右子树k-1层节点数的和
    return GetLevelNums(T->lchild, k-1) + GetLevelNums(T->rchild, k-1);
}//GetLevelNums

//先序遍历二叉树
Status PreOrderTraverse(BiTree T){
    if(T){ //判T是否为空树
        cout<<T->date<<" "; //输出T节点的数据
        if(PreOrderTraverse(T->lchild)); //递归遍历左子树
            if(PreOrderTraverse(T->rchild)); //递归遍历右子树
        return ERROR;
    }else{
        return OK;
    }

}//PreOrderTraverse



//中序遍历二叉树
Status InOrderTraverse(BiTree T){
   if(T){
        if(PreOrderTraverse(T->lchild));
        cout<<T->date<<" ";
            if(PreOrderTraverse(T->rchild));
        return ERROR;
    }else{
        return OK;
    }
}//InOrderTraverse


//后序遍历二叉树
Status PostOrderTraverse(BiTree T){
    if(T){
        if(PreOrderTraverse(T->lchild));
            if(PreOrderTraverse(T->rchild));
             cout<<T->date<<" ";
        return ERROR;
    }else{
        return OK;
    }
}//PostOrderTraverse

main.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include "base.h"
#include "biTree.h"
#include "stack.h" 

//非递归中序遍历二叉树
Status InOrderTraverse_Stack(BiTree T){
    PLinkStack S; //定义一个栈S
    BiTree p = T; //定义一个二叉树节点p = T；
    InitStack_L(&S); //初始化栈S
    while( p || !StackEmpty_L(S)){ //结束条件为二叉树P空且栈S空
        if(p){   //判二叉树p是否为空
            Push_L(S, p);  //根指针进栈遍历左子树
            p = p->lchild; //遍历左子树
        }else{
            Pop_L(S, p); //根指针退栈
            cout<<p->date<<" "; //访问根节点的数据
            p = p->rchild; //遍历右子树
        }//else
    }//while
    return OK;
}//InOrderTraverse_Stack

int main(){

    BiTree T;
    cout<<"先序创建二叉树，请按先序输入二叉树各节点的值：（@字符表示空格）"<<endl;
    CreateBiTree(T);
    cout<<"判空：";
    if(BiTreeEmpty(T))
        cout<<"二叉树为空！"<<endl;
    else
        cout<<"二叉树不为空！"<<endl;
    cout<<"先序遍历二叉树：";
    PreOrderTraverse(T);
    cout<<endl;
    cout<<"中序遍历二叉树：";
    InOrderTraverse(T);
    cout<<endl;
    cout<<"后序遍历二叉树：";
    PostOrderTraverse(T);
    cout<<endl;
    cout<<"非递归中序遍历：";
    InOrderTraverse_Stack(T);
    cout<<endl;
    cout<<"二叉树的深度："<<BiTreeDepth(T)<<endl;
    cout<<"二叉树的叶子数："<<BiTreeLeafCount(T)<<endl;
    cout<<"二叉树的节点数："<<NodeCount(T)<<endl;
    cout<<"第2层的节点数："<<GetLevelNums(T, 2)<<endl;
    cout<<"初始化二叉树："<<endl;
    InitBiTree(T);
    cout<<"销毁二叉树："<<endl;
    return OK;
}

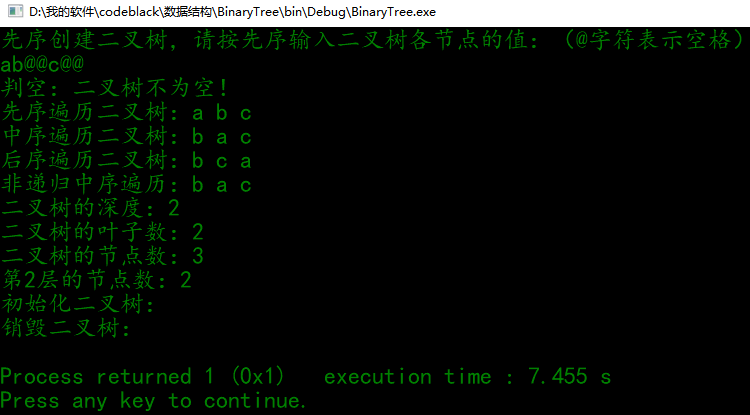
二叉树程序测试结果：

二叉树

图：二叉树程序测试图

坚持原创技术分享，您的支持将鼓励我继续创作！