一元多项式的表示及相加

设计目的与要求

题目与设计要求

我们设计的程序为一元多项式的表示及相加，这是使用C++语言写成。我们使用计算机处理的对象之间通常存在着的是一种最简单的线性关系，这类数学模型可称为线性的数据结构。而数据存储结构有两种：顺序存储结构和链式存储结构。线性表是最常用且最简单的一种数据结构。所以我们做的是———–一元多项式的表示及相加，其过程其实是对线性标的操作。实验结构和链接存储结构上的运算以及熟练运用掌握的线性表的操作，实现一元n次多项式的目的是掌握线性表的基本操作，插入、删除、查找，以及线性表合并等运算在顺序存储的加法运算。学习实现一元n次多项式的加法是符号多项式的操作，是表处理的典型用例，需要注意的是：顺序存储结构指的是用数组方法，使用数组方法实现时，在插入和删除的方面，数组不如链表灵活，方法复杂，删除其中一个需要将其后的数组元素改变位置，使其数组保持原有的顺序结构，在查找方面较链表简单，只需要知道其下标就可以知道。链接存储结构指的是用链表方法,值得注意的是，删除和插入较为灵活，不需要变动大多数元素，但是查找过程相对于数组这种顺序存储结构来说较为复杂，耗时巨大。在这里我们在一元多项式的表示与相加实验中，采用的是链式存储结构。

我们程序的任务是：实现一元多项式：Rn(x)=Pn(x)+Qn(x)

本程序涉及的知识点

1	If语句 switch语句 for循坏 do…while循坏指针结构体函数的套用线性表的操作线性表链式存储结构对内存空间的开辟与释放

功能设计

总体设计

我们需要实现的功能是一元多项式的表示及相加。但在实现一元多项式的过程中，主要是通过对链表的操作来完成的。所以，这里还实现的对链式线性表的基本操作。例如，插入、删除、查找等。对于一元多项式，需要实现一元多项式的创建，同时可以打印出一元多项式，可以对两个多项式进行加法运算。

详细设计

（1）项目工程文件规划：

在这个项目中，我设计使用三个头文件，和一个cpp源文件。以下为各个文件的主要作用：

Base.h：

这个头文件中主要用来存放一些项目需要的头文件和公用的常量和类型。并且一元多项式的存储结构也放在这里。

LinkList.h：

这个头文件为链表头文件，其中主要包含了链式线性表的存储结构和链式线性表的各函数具体实现代码。在这个头文件中实现的方法有：InitList(); MakeNode(); FreeNode();InsFirst(); GetHead(); SetCurElem(); LocateElemP(); NextPos(); GetCurElem(); DelFirst();ListEmpty(); Append(); ListTraverse();

Polynomial.h：

这个头文件是一元多项式头文件，其中主要包含了一元多项式的基本操作的各种方法的实现代码。在这个头文件中实现的方法有：CreatPolyn(); DestroyPolyn(); PolynLength(); PrintPolyn(); AddPolyn();

Main.cpp:

这是一个cpp源文件，也是程序测试文件。它的功能主要是对一元多项式方法的测试，检测所需功能是否完成。

（2）程序存储结构的设计：

链表存储结构：

//----------链表的存储结构表示------------

typedef struct LNode{//节点类型
  ElemType  data;//这里表示了每一项，其指数和系数   struct LNode *next;
}*Link,*Position;

typedef struct{//链表类型
   Link head, tail;//分别指向线性链表中的头结点和最后一个结点
   int len;//指示线性链表中数据元素的个数
}LinkList;//每一项组成一个列表

一元多项式存储结构：

//---------------一元多项式存储结构表示-----------
typedef struct{//项的表示，多项式的项作为LinkList的数据元素
   float coef;//系数
   int expn;//指数
}term, ElemType;//两个类型：term用于本ADT，ElemType为LinkList的数据对象名
typedef LinkList polynomial;

一元多项式其实就是通过链式线性表来存放。通过对线性表的操作进而实现对一元多项式的操作。

程序主要方法的实现

创建多项式的实现：

这是一元多项式程序中主要一个方法，通过它来创建一元多项式。在这个函数中首先会要求传入需要创建几项多项式。然后会通过循环输入每项的系数和指数来生成多项式。其实也就是生成一个按指数升序的链表，以方便后面做一元多项式的加法运算。

在创建一元多项式中，考虑到了用户输入数据的多种情况：每种情况都做了相应的输入策略，每次在插入一个数据项时，首先都会查找是否存在该指数项。如果不存在，然后判断系数是否为0.如果为0，不添加，进行下一次循环。如果不为0，则正常添加一个节点。这个结点是在升序链表中找到适合的位置进入插入，而不是随便添加结点。如果在添加查找该指数时，发现该指数项已经存在，则在原来该指数项的系数上添加上该系数。如果添加后系数等于0.则删除该结点。不为0，则正常进入下一次循环，添加其他数据项。

以下为此函数具体实现代码：

void CreatPolyn(polynomial &p,int m){
    //输入m项的系数和指数，建立表示一元多项式的有序链表P
    InitList(&p);//初始化-多项式链表
    Link h = GetHead(p);//设置头结点的数据元素
    ElemType e;//头结点设置
    Position q,s;
    e.coef = 0.0; e.expn = -1; SetCurElem(h, e);//设置头结点的元素
    for (int i = 1; i <= m; ++i)//依次输入m个非零项
    {
        cout << "第"<<i<<"项的系数:";
        cin >> e.coef;
        cout << "第" << i << "项的指数:";
        cin >> e.expn;
        if (!LocateElemP(p, e,&q, cmp))//当前链表中不存在该指数项
        {
            if (e.coef != 0)//不等于才插入
                if (MakeNode(&s, e))
                    InsFirst(&p,q,s);//生成结点并插入链表
        }
        else//当前链表中存在该指数项,增加其系数
        {
            q->data.coef = q->data.coef + e.coef;
            //如果合起来等于0，则删除掉
            if (q->data.coef == 0)
                Remove_Polyn(&p, q);//删除掉当前节点
        }
    }
}//CreatPolyn

一元多项式相加的具体实现：

在一元多项式相加的函数中。首先会要求传入两个已经创建好的一元多项式PA，PB，然后进行相加，实现PA=PA+PB的功能。

程序执行过程：只有在Pa和Pb都不为空的时候程序才会进行循环，因为一元多项式以链式线性表以指数升序存储。所以每次进入循环都会首先比较Pa和Pb中的需要比较的qa和qb中指数的大小。如果qa的指数小，则会ha和qa指针都后移，继续比较。如果qa和qb的指数相等，则会把qa和qb的系数进行相加并赋值给qa的系数。从而实现相同指数的系数相加，加完后将qb所指结点删除，同时qa后qb指针都后移。如果qa的指数比qb大，则把qb所在的结点链接到qa的前面。qb指针继续后移。进行循环。这是就这个加法的具体实现过程。在最后，如果qa已经为空，而qb不为空，则把qb剩下的结点都直接链接在PA的最后。释放hb的头结点。

void AddPolyn(polynomial &Pa, polynomial &Pb){
    //多项式加法:Pa = Pa+Pb,利用两个多项式的结点构成“和多项式”
    Position ha, hb, qa, qb;
    term a, b;
    ha = GetHead(Pa); hb = GetHead(Pb);//ha和hb分别指向Pa和Pb的头结点
    qa = NextPos(ha); qb = NextPos(hb);//qa和qb分别指向Pa和Pb中的当前结点
                                       //此时qa和qb都是指向多项式第一项
    while (qa && qb)//qa和qb非空
    {
        a = GetCurElem(qa);
        b = GetCurElem(qb); // a和b为两表中当前比较元素
        float sum;
        switch (cmp(a, b))//比较两者的指数值
        {
        case -1://多项式中PA中的结点的指数小
            ha = qa;
            qa = NextPos(ha);
            break;
        case 0://两者指数值相等
            sum = a.coef + b.coef;
            if (sum != 0)
            {
                //修改pa指向的该结点的系数值
                qa->data.coef = sum;
                //下一个
                ha = qa;
            }
            else
            {
                //删除结点
                DelFirst(&Pa, ha, &qa);
                FreeNode(&qa);
            }
            DelFirst(&Pb, hb, &qb);//也删除掉qb的结点
            FreeNode(&qb);//释放qb的空间
            //都往后移动一位
            qb = NextPos(hb);
            qa = NextPos(ha);
            break;
        case 1://多项式PB中的当前结点指数值小
            DelFirst(&Pb, hb, &qb);//把当前结点从PB中删除，并用qb指向当前结点用以插入
            InsFirst(&Pa, ha, qb);//插入在ha前
            qb = NextPos(hb);
            qa = NextPos(ha);
            break;
        }//switch
    }//while
    if (!ListEmpty(Pb))
        Append(&Pa, qb);//连接Pb中剩余结点
    FreeNode(&hb);//释放Pb的头结点
}//AddPolyn

打印多项式的具体实现:

在这个函数，主要调用了ListTraverse()，即对链表进行遍历。通过循环，输出每个结点的数据。循环的次数为一元多项式这个链表的项数。每次输出数据时，调用visit(()函数，在visit函数中，我对输入的各种可能系数和指数进行了情况输出。如果系数为1，则不输出系数。如果系数和指数为负数，则会输出括号，在括号内输出负数。如果指数为1，则不输出指数。如果指数为0，则该项为常数，只输出系数。

void PrintPolyn(polynomialp){
   //打印出一元多项式
    ListTraverse(p, visit);
}
Status ListTraverse(LinkList L, void(*visit)(ElemType)){
    // 依次对L的每个数据元素调用函数visit()。一旦visit()失败，则操作失败
    Link p = L.head->next;
    int j;
    for (j = 1; j <= L.len; j++)
    {
        visit(p->data);
        p = p->next;
    }
    cout << "\b "; //退格，每次输出多项式后删掉的最后输出的"+"
    if (L.len == 0)
        cout << "0";
    return OK;
}//ListTraverse

void visit(ElemType e){
    if (e.coef > 0 && e.coef != 1 && e.expn != 0)
    {
        if(e.expn == 1)
            cout<< e.coef << "x+";
        else if (e.expn > 0)
            cout << e.coef << "x^" << e.expn << "+";
        else
            cout << e.coef << "x^(" << e.expn << ")+";
    }
    else if (e.coef < 0 && e.expn != 0)
    {
        if(e.expn == 1)
            cout<< "(" <<e.coef << ")x+";
        else if (e.expn > 0)
            cout << "(" << e.coef << ")x^" << e.expn << "+";
        else
            cout << "(" << e.coef << ")x^(" << e.expn << ")+";
    }
    else if (e.coef == 1 && e.expn != 0)
    {
        if(e.expn == 1)
            cout<< "x+";
        else if (e.expn > 0)
            cout << "x^" << e.expn << "+";
        else
            cout << "x^(" << e.expn << ")+";
    }
    else if (e.expn == 0 && e.coef != 0)
        cout << e.coef<<"+";
    else
        cout << "";//考虑用户输入可能有系数为0的情况
}//visit

程序测试结果

这里对程序使用了三组数据进行测试：

第一组测试：

第一组测试数据为指数和系数都是正整数的情况。例：PA=3+4x+3x^2 +4x^4; PB=4+6x^2 +3x^4 +3x^5;求PA=PA+PB。如下图4.1:

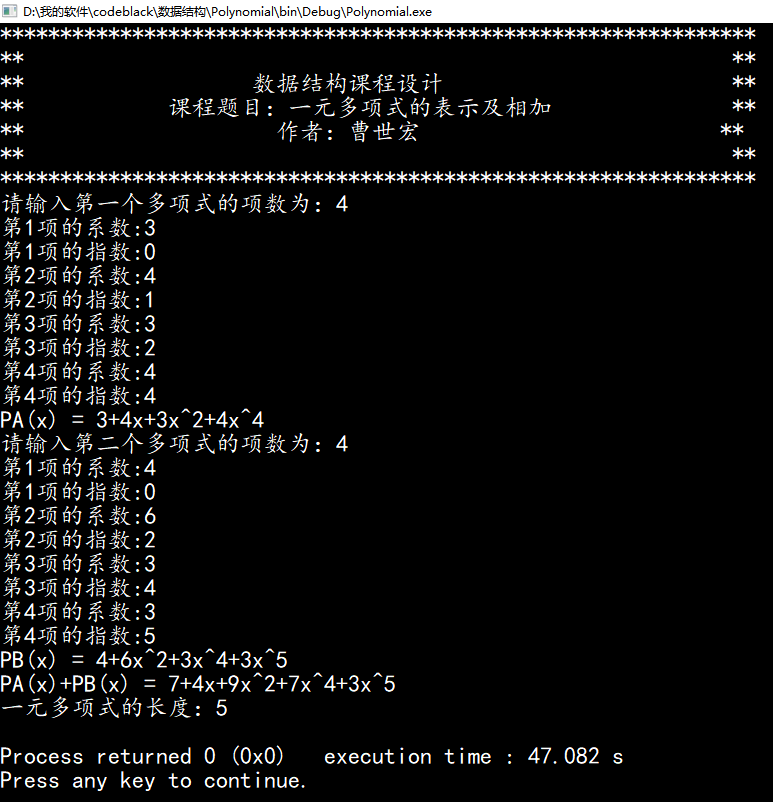
第一组测试程序

图4.1：第一组测试结果

第二组测试：

第二组测试数据为指系数和指数中都有负数的情况。有负数时，会在负数上加上括号来显示。例：PA=-5x^(-2) +4-3x^2 +4x^3; PB=3x^(-3) +3x^2 -4x^3; 求PA=PA+PB；测试结果如下图4.2：

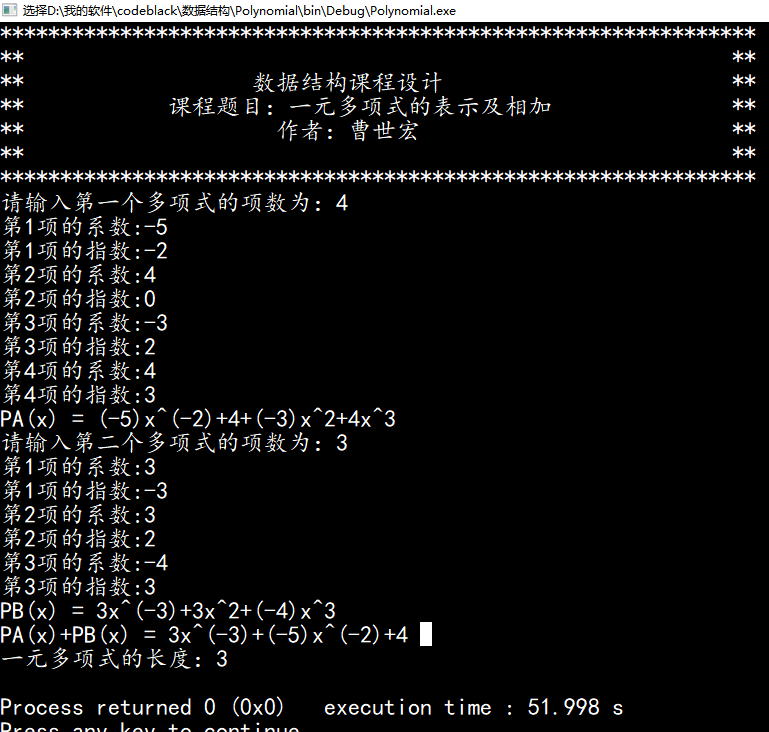
第二组测试程序

图4.2：第二组测试结果

第三组测试：

第三组测试数据为：系数中存在0的情况，和指数中存在1的情况。系数中存在0，在程序执行过程中会自动删除该项。指数为1的时候，该多项式不会显示指数项。例：PA=4+0x^3 +4x^4 -3x^5; PB=3+x^1 +3x^3 +4x^5; 求PA=PA+PB；测试结果如下图4.3：

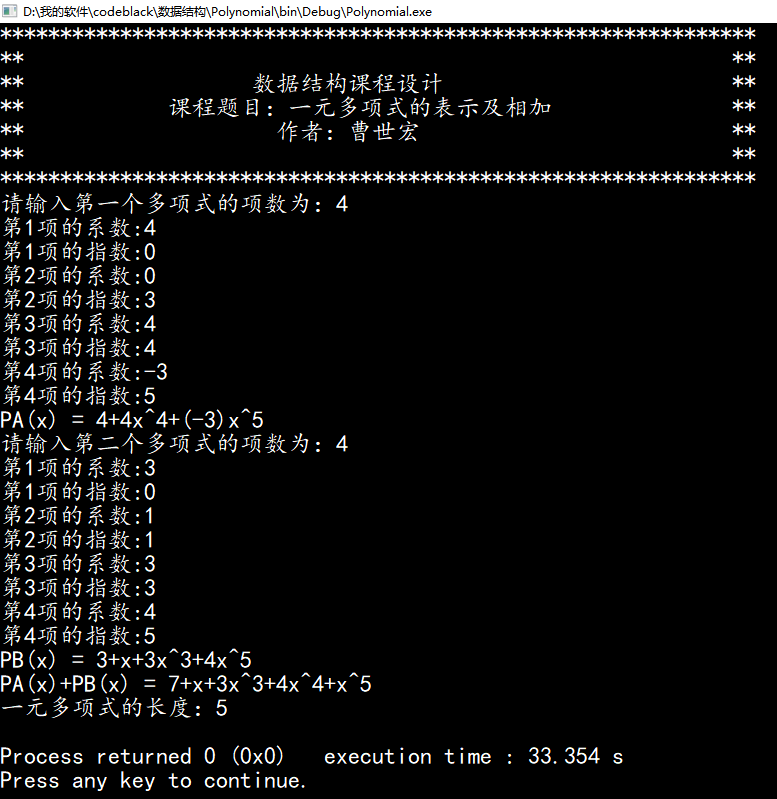
第三组测试程序

图4.3：第三组测试结果

总结：

在做这个程序过程中，我遇到过很多问题，比如有时候调试可以通过，然而程序却不能正确执行，总会出错。这种情况只能去仔细检查对应代码的逻辑是否有错误。把可能出现的情况去修改，然后慢慢去调试。通过这样的反复调试，我感觉对线性链表的知识理解更加深刻。同时，对写代码也有了很多练习，写的代码更规范，更简洁。在这个实验过程中，也与我的小组队员进行了多次讨论，让我们懂得了团队合作的重要性。通过小组讨论，使我对一些模糊不清的地方了解透彻，同时小组其他成员也都理解了相应的知识。最后，通过这个实验，使我对链式线性表可以很熟练的去运用。同时，对一元多项式的简单操作也有了清晰的认识。只有经常进行编程练习，我们的编程能力才能得到有效提高。

全部代码：

base.h

//base.h

//----常用的头文件--------
#include <iostream>
using namespace std;
#include <malloc.h>

//-----公用的常量和类型----------
#define   OK                    1
#define   ERROR                 0
#define   OVERFLOW             -2
#define   TRUE                  1
#define   FALSE                 0

typedef   int   Status;

//---------一元多项式存储结构表示----------
typedef struct{//项的表示，多项式的项作为LinkList的数据元素
    float coef;//系数
    int expn;//指数
}term, ElemType;//两个类型：term用于本ADT，ElemType为LinkList的数据对象名

LinkList.h

//LinkList.h
//链式表的基本函数实现

//----------链表的存储结构表示------------
typedef struct LNode{//节点类型
    ElemType  data;//这里表示了每一项，其指数和系数
    struct LNode *next;
}*Link,*Position;
typedef struct{//链表类型
    Link head, tail;//分别指向线性链表中的头结点和最后一个结点
    int len;//指示线性链表中数据元素的个数
}LinkList;//每一项组成一个列表

//----------链表函数的具体实现代码-----------
Status InitList(LinkList *L){
    // 构造一个空的线性链表
    Link p;
    p = (Link)malloc(sizeof(LNode)); // 生成头结点
    if (p)
    {
        p->next = NULL;
        (*L).head = (*L).tail = p;
        (*L).len = 0;
        return OK;
    }
    else
        return ERROR;//内存分配不够
}//InitList

Status MakeNode(Link *p, ElemType e){
    // 分配由p指向的值为e的结点，并返回OK；若分配失败。则返回ERROR
    *p = (Link)malloc(sizeof(LNode));
    if (!*p)
        return ERROR;
    (*p)->data = e;
    return OK;
}//MakeNode

void FreeNode(Link *p){
    // 释放p所指结点
    free(*p);
    *p = NULL;
}//FreeNode

Status InsFirst(LinkList *L, Link h, Link s){
 // h指向L的一个结点，把h当做头结点，将s所指结点插入在第一个结点之前
    s->next = h->next;
    h->next = s;
    if (h == (*L).tail) // h指向尾结点
        (*L).tail = h->next; // 修改尾指针
    (*L).len++;
    return OK;
}//InsFirst

Position GetHead(LinkList L){
    // 返回线性链表L中头结点的位置
    return L.head;
}//GetHead

Status SetCurElem(Link p, ElemType e){
    // 已知p指向线性链表中的一个结点，用e更新p所指结点中数据元素的值
    p->data = e;
    return OK;
}//SetCurElem

Status LocateElemP(LinkList L, ElemType e, Position *q, int(*compare)(ElemType, ElemType)){
     // 若升序链表L中存在与e满足判定函数compare()取值为0的元素，则q指示L中
    // 第一个值为e的结点的位置，并返回TRUE；否则q指示第一个与e满足判定函数
    // compare()取值>0的元素的前驱的位置。并返回FALSE。（用于一元多项式）
    Link p = L.head, pp;
    do
    {
        pp = p;
        p = p->next;
    } while (p && (compare(p->data, e)<0)); // 没到表尾且p->data.expn<e.expn
    if (!p || compare(p->data, e)>0) // 到表尾或compare(p->data,e)>0
    {
        *q = pp;
        return FALSE;
    }
    else // 找到
    {// 没到表尾且p->data.expn=e.expn
        *q = p;
        return TRUE;
    }
}//LocateElemP

Position NextPos(Link p){
   // 已知p指向线性链表L中的一个结点，返回p所指结点的直接后继的位置
   //  若无后继，则返回NULL
    return p->next;
}//NextPos

ElemType GetCurElem(Link p){
     // 已知p指向线性链表中的一个结点，返回p所指结点中数据元素的值
    return p->data;
}//GetCurElem

Status DelFirst(LinkList *L, Link h, Link *q){ // 形参增加L,因为需修改L
  // h指向L的一个结点，把h当做头结点，删除链表中的第一个结点并以q返回。
  // 若链表为空(h指向尾结点)，q=NULL，返回FALSE
    *q = h->next;
    if (*q) // 链表非空
    {
        h->next = (*q)->next;
        if (!h->next) // 删除尾结点
            (*L).tail = h; // 修改尾指针
        (*L).len--;
        return OK;
    }
    else
        return FALSE; // 链表空
}//DelFirst

Status ListEmpty(LinkList L){
    // 若线性链表L为空表，则返回TRUE，否则返回FALSE
    if (L.len)
        return FALSE;
    else
        return TRUE;
}//ListEmpty

Status Append(LinkList *L, Link s){
  // 将指针s(s->data为第一个数据元素)所指(彼此以指针相链,以NULL结尾)的
  //  一串结点链接在线性链表L的最后一个结点之后,并改变链表L的尾指针指向新
  //  的尾结点
    int i = 1;
    (*L).tail->next = s;
    while (s->next)
    {
        s = s->next;
        i++;
    }
    (*L).tail = s;
    (*L).len += i;
    return OK;
}//Append

Status ListTraverse(LinkList L, void(*visit)(ElemType)){
    // 依次对L的每个数据元素调用函数visit()。一旦visit()失败，则操作失败
    Link p = L.head->next;
    int j;
    for (j = 1; j <= L.len; j++)
    {
        visit(p->data);
        p = p->next;
    }
    cout << "\b "; //退格，每次输出多项式后删掉的最后输出的"+"
    if (L.len == 0)
        cout << "0";
    return OK;
}//ListTraverse

void visit(ElemType e){
    if (e.coef > 0 && e.coef != 1 && e.expn != 0)
    {
        if(e.expn == 1)
            cout<< e.coef << "x+";
        else if (e.expn > 0)
            cout << e.coef << "x^" << e.expn << "+";
        else
            cout << e.coef << "x^(" << e.expn << ")+";
    }
    else if (e.coef < 0 && e.expn != 0)
    {
        if(e.expn == 1)
            cout<< "(" <<e.coef << ")x+";
        else if (e.expn > 0)
            cout << "(" << e.coef << ")x^" << e.expn << "+";
        else
            cout << "(" << e.coef << ")x^(" << e.expn << ")+";
    }
    else if (e.coef == 1 && e.expn != 0)
    {
        if(e.expn == 1)
            cout<< "x+";
        else if (e.expn > 0)
            cout << "x^" << e.expn << "+";
        else
            cout << "x^(" << e.expn << ")+";
    }
    else if (e.expn == 0 && e.coef != 0)
        cout << e.coef<<"+";
    else
        cout << "";//考虑用户输入可能有系数为0的情况
}//visit

Polynomial.h

//Polynomial.h
//一元多项式基本操作头文件

typedef LinkList polynomial;

Status Remove_Polyn(LinkList *L, Link q){
    //由于项的指数为0，删除掉已有的项
    Link  h;
    h = L->head;
    while (h->next != q)
    {
        h = h->next;
    }
    //找到了
    if (q == L->tail)
    {//删除的如果是表尾，改变表尾
        L->tail = h;
    }
    h->next = q->next;
    free(q);
    L->len--;
    return OK;
}//Remove_Polyn

int cmp(term a, term b){// CreatPolyn()的实参
 // 依a的指数值<、=或>b的指数值，分别返回-1、0或+1
    if (a.expn == b.expn)
        return 0;
    else if(a.expn > b.expn)
        return 1;
    else
        return -1;
}//cmp

void CreatPolyn(polynomial &p,int m){
    //输入m项的系数和指数，建立表示一元多项式的有序链表P
    InitList(&p);//初始化-多项式链表
    Link h = GetHead(p);//设置头结点的数据元素
    ElemType e;//头结点设置
    Position q,s;
    e.coef = 0.0; e.expn = -1; SetCurElem(h, e);//设置头结点的元素
    for (int i = 1; i <= m; ++i)//依次输入m个非零项
    {
        cout << "第"<<i<<"项的系数:";
        cin >> e.coef;
        cout << "第" << i << "项的指数:";
        cin >> e.expn;
        if (!LocateElemP(p, e,&q, cmp))//当前链表中不存在该指数项
        {
            if (e.coef != 0)//不等于才插入
                if (MakeNode(&s, e))
                    InsFirst(&p,q,s);//生成结点并插入链表
        }
        else//当前链表中存在该指数项,增加其系数
        {
            q->data.coef = q->data.coef + e.coef;
            //如果合起来等于0，则删除掉
            if (q->data.coef == 0)
                Remove_Polyn(&p, q);//删除掉当前节点
        }
    }
}//CreatPolyn

void DestroyPolyn(polynomial &p){
    //销毁一元多项式
    Link h,s;
    h = p.head;
    while(h){
        s = h;
        h = h->next;
        FreeNode(&s);
    }
    p.head = p.tail = NULL;
}//DestroyPolyn


int PolynLength(polynomial p){
    //返回一元多项式的长度
    return p.len;
}//PolynLength

void PrintPolyn(polynomial p){
    //打印出一元多项式
    ListTraverse(p, visit);
}
void AddPolyn(polynomial &Pa, polynomial &Pb){
    //多项式加法:Pa = Pa+Pb,利用两个多项式的结点构成“和多项式”
    Position ha, hb, qa, qb;
    term a, b;
    ha = GetHead(Pa); hb = GetHead(Pb);//ha和hb分别指向Pa和Pb的头结点
    qa = NextPos(ha); qb = NextPos(hb);//qa和qb分别指向Pa和Pb中的当前结点
                                       //此时qa和qb都是指向多项式第一项
    while (qa && qb)//qa和qb非空
    {
        a = GetCurElem(qa);
        b = GetCurElem(qb); // a和b为两表中当前比较元素
        float sum;
        switch (cmp(a, b))//比较两者的指数值
        {
        case -1://多项式中PA中的结点的指数小
            ha = qa;
            qa = NextPos(ha);
            break;
        case 0://两者指数值相等
            sum = a.coef + b.coef;
            if (sum != 0)
            {
                //修改pa指向的该结点的系数值
                qa->data.coef = sum;
                //下一个
                ha = qa;
            }
            else
            {
                //删除结点
                DelFirst(&Pa, ha, &qa);
                FreeNode(&qa);
            }
            DelFirst(&Pb, hb, &qb);//也删除掉qb的结点
            FreeNode(&qb);//释放qb的空间
            //都往后移动一位
            qb = NextPos(hb);
            qa = NextPos(ha);
            break;
        case 1://多项式PB中的当前结点指数值小
            DelFirst(&Pb, hb, &qb);//把当前结点从PB中删除，并用qb指向当前结点用以插入
            InsFirst(&Pa, ha, qb);//插入在ha前
            qb = NextPos(hb);
            qa = NextPos(ha);
            break;
        }//switch
    }//while
    if (!ListEmpty(Pb))
        Append(&Pa, qb);//连接Pb中剩余结点
    FreeNode(&hb);//释放Pb的头结点
}//AddPolyn

Main.cpp

#include "base.h"
#include "LinkList.h"
#include "Polynomial.h"

int main()
{
    cout<<"***************************************************************"<<endl;
    cout<<"**                                                           **"<<endl;
    cout<<"**                   数据结构课程设计                        **"<<endl;
    cout<<"**            课程题目：一元多项式的表示及相加               **"<<endl;
    cout<<"**                     作者：曹世宏                          **"<<endl;
    cout<<"**                                                           **"<<endl;
    cout<<"***************************************************************"<<endl;
    polynomial A, B;
    cout << "请输入第一个多项式的项数为：";
    int length; //一元多项式项数
    cin >> length;
    CreatPolyn(A, length);
    //显示A出来
    cout << "PA(x) = ";
    PrintPolyn(A);//打印一元多项式
    cout << endl;
    //输入B
    cout << "请输入第二个多项式的项数为：";
    cin >> length;
    CreatPolyn(B, length);
    //输出B
    cout << "PB(x) = ";
    PrintPolyn(B);
    cout << endl;
    //假设以上输入成功
    //进行相加
    AddPolyn(A, B);//一元多项式相加
    //这时候A是合并后的结果
    cout << "PA(x)+PB(x) = ";
    PrintPolyn(A);
    cout << endl;
    cout<<"一元多项式的长度："<<PolynLength(A)<<endl;
    DestroyPolyn(A);
    return 0;
}