深度优先遍历和广度优先遍历

发表于 | 分类于 | 阅读次数： | 字数： 1,517 | 阅读时长： 8

深度优先遍历

深度优先遍历(Depth-First Traversal)简称DFS。

算法思想：

  1. 首先以一个未被访问过的顶点作为起始顶点，沿当前顶点的边走到未访问过的顶点；
  2. 当没有未访问过的顶点时，则回到上一个顶点，继续试探别的顶点，直到所有的顶点都被访问过。

深度

图：深度优先遍历示例图

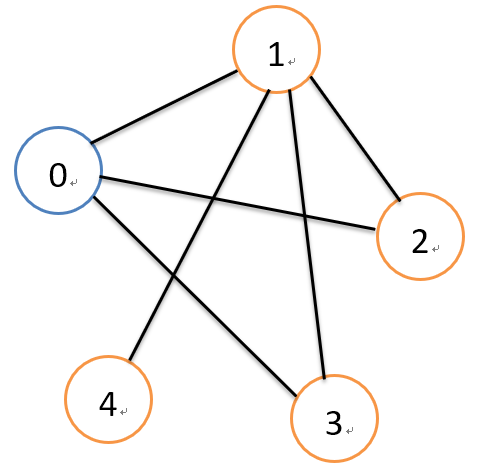
如上图，采用图的深度优先遍历的话，从0号节点遍历的顺序应该是：0,1,2,3,4.

程序源代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class DeepTravel {

	public static void main(String[] args) {	
		//图的邻接矩阵表示
		int[][] a = {
				{0,1,1,1,0},
				{1,0,1,1,1},
				{1,1,0,0,0},
				{1,1,0,0,0},
				{0,1,0,0,0}};
		//需要一个数字，来记录染色信息，染色的节点代表已经遍历
		int[] color = new int[a.length];
		System.out.println("深度优先遍历的结果为：");
		dfs(a, color, 0);
	}

	//用递归的方法进行遍历
	private static void dfs(int[][] a, int[] color, int k) {
		System.out.print(k + " ");//打印出k号节点
		color[k] = 1;//给k号节点标记为1
		
		for(int i = 0; i < a[k].length; i++)
			if(a[k][i] == 1 && color[i] == 0)
				dfs(a, color, i);
	}
}

程序运行结果：

1
2
深度优先遍历的结果为：
0 1 2 3 4

广度优先遍历

广度优先搜索算法（英语：Breadth-First-Search，缩写为BFS）。

其过程检验来说是对每一层节点依次访问，访问完一层进入下一层，而且每个节点只能访问一次。

程序示例：

广度

图：广度优先遍历示例图

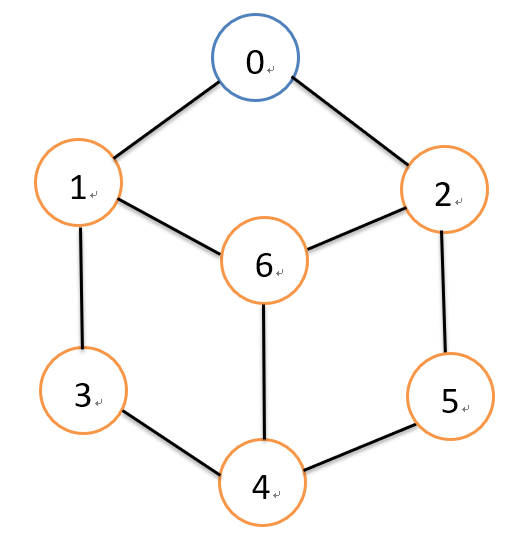
如上图，，采用图的广度优先遍历的话，从0号节点遍历的顺序应该是：0,1,2,3,6,5,4

程序源代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import java.util.ArrayList;
import java.util.HashSet;
import java.util.Set;

public class BreadthTravel {

	public static void main(String[] args) {
		//图的邻接定义
		int[][] g = {
				{0,1,1,0,0,0,0},
				{1,0,0,1,0,0,1},
				{1,0,0,0,0,1,1},
				{0,1,0,0,1,0,0},
				{0,0,0,1,0,1,1},
				{0,0,1,0,1,0,0},
				{0,1,1,0,1,0,0}};
		
		//广度优先遍历
		System.out.println("广度优先遍历的结果：");
		bfs(g);
		
	}

	private static void bfs(int[][] g) {
		ArrayList<Integer> list = new ArrayList<Integer>();//等待遍历的节点
		Set<Integer> set = new HashSet<Integer>();//已经遍历的节点
		list.add(0);//从0号节点开始遍历
		
		while (true) {
			//如果列表为空，则遍历完成
			if(list.isEmpty())
				break;
			
			int node = list.get(0);
			System.out.print(node + " ");
			set.add(node);
			list.remove(0);
			
			for(int i = 0; i < g[node].length; i++) {
				if(g[node][i] == 1 && set.contains(i) == false && list.indexOf(i)<0)
					list.add(i);
			}			
		}
	}
}

程序运行结果：

1
2
广度优先遍历的结果：
0 1 2 3 6 5 4

最短路径树

迪杰斯特拉算法简介

迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

程序示例：

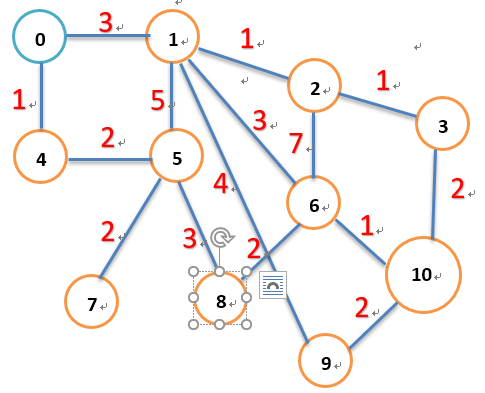
最短路径树

图：最短路径树示例拓扑

如上图，从求0号节点开始到所有节点的最短路径。

程序源代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
import java.util.ArrayList;
import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;

public class 最短路径树 {

	static class Cell{
		int node; //连接到哪个节点
		int weight; //边的权值
		
		public Cell(int node, int weight) {
			this.node = node;
			this.weight = weight;
		}
	}
	@SuppressWarnings("unchecked")
	public static void main(String[] args) {
		//图的邻接表
		ArrayList[] g = new ArrayList[11];		
		for(int i = 0; i < g.length; i++)
			g[i] = new ArrayList();
		
		g[0].add(new Cell(1, 3));
		g[0].add(new Cell(4, 1));
		g[1].add(new Cell(2, 1));
		g[1].add(new Cell(6, 3));
		g[1].add(new Cell(5, 5));
		g[1].add(new Cell(0, 3));
		g[1].add(new Cell(9, 4));
		g[2].add(new Cell(1, 1));
		g[2].add(new Cell(3, 1));
		g[2].add(new Cell(6, 7));
		g[3].add(new Cell(2, 1));
		g[3].add(new Cell(10, 2));
		g[4].add(new Cell(0, 1));
		g[4].add(new Cell(5, 2));
		g[5].add(new Cell(4, 2));
		g[5].add(new Cell(1, 5));
		g[5].add(new Cell(7, 2));
		g[5].add(new Cell(8, 3));
		g[6].add(new Cell(1, 3));
		g[6].add(new Cell(2, 3));
		g[6].add(new Cell(8, 2));
		g[6].add(new Cell(10, 1));
		g[7].add(new Cell(5, 2));
		g[8].add(new Cell(5, 3));
		g[8].add(new Cell(6, 2));
		g[9].add(new Cell(1, 4));
		g[9].add(new Cell(10, 2));
		g[10].add(new Cell(3, 2));
		g[10].add(new Cell(6, 1));
		g[10].add(new Cell(9, 2));
		
		//求0号节点开始的所有最小路径
		Dijkstra(g);
		
	}
	public static void Dijkstra(ArrayList[] g) {
		//节点号-->最小路径值
		Map<Integer, Integer> map = new HashMap<Integer, Integer>();
		
		while(true) {
			int min = Integer.MAX_VALUE; //最小路径值
			int min_no = -1; //对应的节点号
			
			//所有与0号节点邻接，并且不在集合map中的点
			for(int i = 0; i < g[0].size(); i++) {
				Cell t = (Cell) g[0].get(i);
				if(map.get(t.node) == null && t.weight < min) {
					min_no = t.node;
					min = t.weight;
				}
			}
			//与map中点邻接的所有不在map中的点
			Iterator it = map.keySet().iterator();
			while(it.hasNext()) {
				int k = (int)it.next();
				//集合中的点对应的最小路径的值
				int v = (int)map.get(k);
				for(int i = 0; i < g[k].size(); i++) {
					Cell t = (Cell)g[k].get(i);
					if(map.get(t.node) == null && t.weight + v < min) {
						min_no = t.node;
						min = t.weight + v;
					}
				}
			}
			
			if(min < Integer.MAX_VALUE)
				map.put(min_no, min);
			else
				break;
		}
		System.out.println(map);
	}
}

程序运行结果：

1
{0=2, 1=3, 2=4, 3=5, 4=1, 5=3, 6=6, 7=5, 8=6, 9=7, 10=7}
坚持原创技术分享，您的支持将鼓励我继续创作！