位运算的奇巧淫技

发表于 | 更新于 | 分类于 | 阅读次数： | 字数： 3,391 | 阅读时长： 15

位运算简介

位运算简介：

​ 程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作。比如，and运算本来是一个逻辑运算符，但整数与整数之间也可以进行and运算。举个例子，6的二进制是110，11的二进制是1011，那么6 and 11的结果就是2，它是二进制对应位进行逻辑运算的结果（0表示False，1表示True，空位都当0处理）。

位运算的特点：

  • 在处理整形数值时，可以直接对组成整形数值的各个位进行操作。这意味着可以使用屏蔽技术获得整个数中的各个位。
  • &（与）、|（或）、^(异或)、~（非/取反）
  • >>和<<运算符将二进制位进行右移或者左移操作。
  • >>>运算符将用0填充高位；>>运算符用符号位填充高位，没有\<<<运算符。
  • 对于int型，1<<35与1<<3是相同的，而左边的操作数是long型是需要对右侧的操作数作数模64。
  • 与：相同为1，或：有一个为1结果为1，异或：相同为0，不同为1.

位运算的规则：

运算

图：位运算的规则

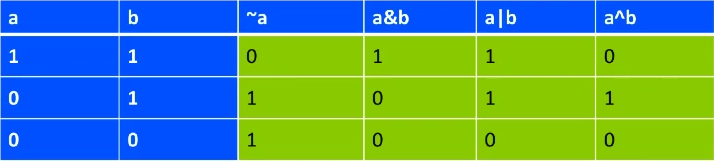
异或的性质：

异或，可以理解为不进位的加法：1+1=0； 0+0=0；1+0=1

  • 交换律：可任意交换运算因子的位置，结果不变。
  • 结合律：即（a^b）^c == a^(b^c)
  • 对于任何数x，都有x^x =0, x^0 = x， 同自己求异或为0，同0求异或为自己。
  • 自反性：A^B^B = A^0=A,连续喝同一个因子做异或运算，最终结果为自己。

位运算的简单应用

判断奇偶数：

思路：

任何整数，如果是奇数，则转化为二进制数后，最后一位二进制位肯定为1，为偶数，则最后一位二进制位为0。利用这个性质，将任意整数x与1作与运算，如果结果为1，则x为奇数；结果为0，则x为0数。

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class Case1_JudjeOddEven {

	public static void main(String[] args) {
		int a = 40;
		int b = 31;
		judjeOddEven(a);
		judjeOddEven(b);
	}
	public static void judjeOddEven(int x) {
		System.out.println( ((x&1) == 0) ? (x + "是偶数！") : (x + "是奇数！") );
	}
}
//-------------------------------------------------------
// 运行结果：
40是偶数！
31是奇数！

获取二进制位是1还是0（两种解决方法）：

思路：

  • 方案1：做与运算。例如：判断x的第五位二进制是1还是0，可以与1<<4做与运算，然后将结果>>4位，判断最终结果是1还是0。如果最终结果是0，则x的第五位为0，否则第五位的二进制位1。

  • 方案2：做与运算。例如：判断x的第五位二进制是1还是0，可以将x>>4位，与1做与运算，判断最终结果是1还是0。如果最终结果是0，则x的第五位为0，否则第五位的二进制位1。

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class Case2_Judje0_1 {

	public static void main(String[] args) {
		judje0_1(10, 2);
		judje0_1(10, 3);
		judje0_1_2(10, 2);
		judje0_1_2(10, 3);
	}
	
	/**
	 * 判断整数x的第y位的二进制位是0还是1
	 * @param x 一个整数x
	 * @param y 判断x的二进制的第几位
	 */
    //方案1代码
	public static void judje0_1(int x ,int y) {
		System.out.println(x + "的第" + y + "位的二进制位为：" + ( ((x & (1<<(y-1)))>>(y-1)) == 0 ? "0":"1"));
	}
	
    //方案2代码
	public static void judje0_1_2(int x ,int y) {
		System.out.println(x + "的第" + y + "位的二进制位为：" + ( ((x>>(y-1)) & 1) == 0 ? "0":"1"));
	}
}

程序运行结果：

1
2
3
4
10的第2位的二进制位为：1
10的第3位的二进制位为：0
10的第2位的二进制位为：1
10的第3位的二进制位为：0

交换两个整数变量的值：

思路：

利用异或的性质实现。对于任何数x，都有x^x =0, x^0 = x， 同自己求异或为0，同0求异或为自己。 自反性：A^B^B = A^0=A,连续喝同一个因子做异或运算，最终结果为自己。如交换A、B的值，有：

  1. A = A ^ B
  2. B = A ^ B （B = A ^ B ^ B = A）
  3. A = A ^ B (A = A ^ A ^ B = B)

代码示例：

1
2
3
4
5
6
7
8
9
10
11
public class Case3_SwapValue {

	public static void main(String[] args) {
		int a = 3, b = 6;
		System.out.println("交换前：a=" + a + " b=" + b);
		a = a ^ b;
		b = a ^ b;
		a = a ^ b;
		System.out.println("交换后：a=" + a + " b=" + b);
	}
}

运行结果：

1
2
交换前：a=3 b=6
交换后：a=6 b=3

不用判断语句，求整数的绝对值：

思路：

利用位运算的移位，异或运算实现。

原理：将一个整型整数x，带符号右移31位，则结果要么是0，要么是-1。其中如果是0，则x为正数，为-1则x为负数。然后，将x与右移31位后的结果做异或运算，当与x^0是，结果还是x。 当x^-1时，结果为x取反，即x的反码，然后+1，即为x的绝对值。

代码示例：

1
2


程序运行结果：

1
2
31的绝对值是：31
-21的绝对值是：21

位运算的例题

题1_找出唯一成对的数：

题目：

​ 1-1000这1000个数放在10001个元素的数组中，只有唯一的一个元素值重复，其他均只出现一次。每个数组元素只能访问一次，设计一个算法，将他找出来；不用辅助存储空间，能否设计一个算法实现？

思路：

利用位运算异或的性质，A^A=0;A^0=A.

将1001个数一起做异或运算，会把相同的那组数去除。但是要找的数为相同的数，所以在和1-1000的每个数做异或，最后就能找到那个数。

代码实现：

为了方便查看结果，测试用了1-10，有一个数重复。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class Case5_唯一成对的数 {

	public static void main(String[] args) {
		int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 5};
		int x = 0;
		//数组中每个数都互相进行异或运算。相同数会被消除
		for(int i = 0; i < arr.length; i++) {
			x = x ^ arr[i];
		}
		//再将异或运算结果与1-10所有数进行异或，就会消除所有不同的数，最后剩下唯一一个数。
		for(int i = 1; i < arr.length; i++) {
			x = x ^ i;
		}
		System.out.println("数组中唯一重复的数是：" + x);
	}
}

程序运算结果：

1
数组中唯一重复的数是：5

题2_找出落单的那个数：

题目：

一个数组里除了某个数字之外，其他的数字都出现了两次。请写程序找出这个只出现了一次的数字。

思路：

和上题思路相同。利用异或，相同的数异或，会消去。

示例代码：

1
2
3
4
5
6
7
8
9
10
public class 找出落单的那个数 {
	public static void main(String[] args) {
		int[] arr = {1, 7, 5, 3, 10, 6, 3, 6, 7, 8, 5, 10, 1};
		int x = 0;
		for(int i = 0; i < arr.length; i++) {
			x = x ^ arr[i];
		}
		System.out.println("落单的那个数是：" + x);
	}
}

程序运行结果：

1
落单的那个数是：8

题3_二进制中1的个数：

题目：

请实现一个函数，输入一个整数，输出该数二进制表示中1的个数。

例：9的二进制表示为1001，有2位是1.

思路：

解题方式有三种方式：与上面判断某位是1还是0思想相同。

方案1：与上面判断某位是1还是0思想相同。第一种方案是：例如：判断x的第五位二进制是1还是0，可以与1<<4做与运算，然后将结果>>4位，判断最终结果是1还是0。如果最终结果是0，则x的第五位为0，否则第五位的二进制位1。然后循环判断每个二进制位。

方案2：做与运算。例如：判断x的第五位二进制是1还是0，可以将x>>4位，与1做与运算，判断最终结果是1还是0。如果最终结果是0，则x的第五位为0，否则第五位的二进制位1。

方案3：（x-1）& x，利用该式可循环消去低位的1，循环了多少次，就有多少个1。原理：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
> 例如9：二进制位1001
> 	1001      //x 
>  -     1 	  //x-1
>  ---------
>  	1000 	 //消去了低位的1
>  &  1001     //(x-1) & x
>  ---------
>     1000     //新的x
>  - 	   1
>  ---------
>  	0111
>  &  1000	// (x-1) & x 
>  ---------
>  	0000	//消去了最后一个1. 
>     		// 循环多少次则该数的二进制有多少个1
>

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public class 二进制中1的个数 {

	public static void main(String[] args) {
		int x = 2352;
		// 输出x的二进制位，作为验证。
		System.out.println(Integer.toBinaryString(x));
		
		// 方案1
		int count = 0; //初始化，用来记录1的个数
		for(int i = 0; i < 32; i++) {
			if(((x&(1<<i))>>i) == 1) {
				count++;
			}
		}
		System.out.println(count);
		
		// 方案2 
		count = 0; //初始化，用来记录1的个数
		for(int i = 0; i < 32; i++) {
			if(((x>>i) & 1) == 1) {
				count++;
			}
		}
		System.out.println(count);
		
		// 方案3
		count = 0;
		while(x != 0) {
			x = ((x-1) & x);
			count++;
		}
		System.out.println(count); 
	}
}

程序运行结果：

1
2
3
4
100100110000
4
4
4

题4_是不是2的整数次方：

题目：

用一条语句判断一个整数是不是2的整数次方。

思路：

思路为上题的方案3.

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class 是不是2的整数次方 {

	public static void main(String[] args) {
		is2(1024);
		is2(1000);
	}
	
	public static void is2(int x){
		if(((x-1) & x) == 0) {
			System.out.println(x + "是2的整数次方！");
		}else {
			System.out.println(x + "不是2的整数次方！");
		}
	}
}

程序运行结果：

1
2
1024是2的整数次方！
1000不是2的整数次方！

题5_将整数的奇偶位互换：

题目：

将一个整数的二进制位上的1与0做交换。

思路：

利用位运算的异或运算和与运算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
> //例如：求10,交换后的数。 10的二进制为：1010
> 
> 								 1010
> & 01010101 01010101 01010101 01010101
> ---------------------------------------
>                x                 0000 //保留奇数位上的数
> 
>                                  1010
> & 10101010 10101010 10101010 10101010
> ---------------------------------------
>                y                  1010 //保留偶数位上的数
>                   
>  (x<<1) ^ (y>>1) = (0000<<1) ^ (1010>>1)
>                  =  0000 ^ 0101
>                  =  0101   //从而实现了，奇偶位互换
>

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class 将整数奇偶位互换 {

	public static void main(String[] args) {
		int n = 10;
		System.out.println(Integer.toBinaryString(n));
		int a = swapOddEven(n);
		System.out.println("10的二进制位交换后变为" + a);
		System.out.println(Integer.toBinaryString(a));
	}
	
	public static int swapOddEven(int n) {
		//消除奇数位，保留偶数位
	    //和01010101 01010101 01010101 01010101做运算
		int x = n & 0x55555555;
		//消除偶数位，保留奇数位
		//和10101010 10101010 10101010 10101010做运算
		int y = n & 0xaaaaaaaa; 
	    return (x<<1)^(y>>1);
	}
}

程序运行结果：

1
2
3
1010
10的二进制位交换后变为5
101

题6_0~1间浮点实数的二进制表示：

题目：

给定一个介于0和1之间的实数，如（0.625），类型为double，打印它的二进制表示（0.101，因为小数点后的二进制分别表示为0.5 , 0.25, 0.125…).

如果该数字无法精确的用32位以内的二进制表示，则打印“ERROR”。

思路：

可以每次讲x * 2，然后去整数部分，如果整数部分为1，则在二进制表示在0. 后面加1，如果为0，则加0. 循环，直到x为0结束。

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class 浮点实数的二进制表示 {

	public static void main(String[] args) {
		double x = 0.625;
		StringBuffer sb = new StringBuffer("0.");
		while(x > 0) {
			// 乘2: 挪整
			double r = x * 2;
			//判断整数部分
			if (r >= 1) {
				sb.append("1");
				// 消除掉整数部分
				x = r - 1;
			}else{
				sb.append("0");
				x = r;
			}
			if(sb.length() > 34) {
				System.out.println("ERROR");
				return;
			}
		}
		System.out.println(sb.toString());
	}
}

程序运行结果：

1
0.101

题7_出现k次与出现1次：

题目：

数组中只有一个数出现了1次，其他的数都出现了K次，请输出只出现了一次的数。

思路：

2个相同的2进制数做不进位加法，结果为0.

10个相同的10进制数做不进位加法，结果为0.

k个相同的k进制数做不进位加法，结果为0.

解题方式：做k进制的不进位加。

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public class 出现K次 {

	public static void main(String[] args) {
		//假设K=3时的解题方法
		int[] arr = {2, 2, 2, 9, 7, 7, 7, 3, 3, 3, 6, 6, 6, 0, 0, 0};
		int len = arr.length;
		// 存取每个数的三进制
		char[][] kRadix = new char[len][];
		int k = 3; //转化k进制字符数组
		//记录转化三进制后最长的长度
		int maxlen = 0;
		//对于每个数字
		for(int i = 0; i < len; i++) {
			kRadix[i] = new StringBuffer(Integer.toString(arr[i], k)).reverse().toString().toCharArray();
			if(kRadix[i].length > maxlen)
				maxlen = kRadix[i].length;
		}
		int[] resArr = new int[maxlen];
		for(int i = 0; i < len; i++) {
			// 不进位加法
			for(int j = 0; j < maxlen; j++) {
				if(j >= kRadix[i].length)
					resArr[j] += 0;
				else
					resArr[j] += (kRadix[i][j] - '0');
			}	
		}
		
		int res = 0;
		for(int i = 0; i < maxlen; i++) {
			res += (resArr[i] % k) * (int)(Math.pow(k, i));
		}
		System.out.println(res);
	}
}

程序运行结果：

1
9
坚持原创技术分享，您的支持将鼓励我继续创作！