多维数组和矩阵程序练习

发表于 | 更新于 | 分类于 | 阅读次数： | 字数： 3,893 | 阅读时长： 19

顺时针打印二维数组：

题目：

顺时针打印二维数组。

例如：将如下数组：

1
2
3
4
5
> {{1, 2, 3, 4},
> {5, 6, 7, 8},
> {9, 10, 11, 12},
> {13, 14, 15, 16}}
>

输出为：1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10

思路：

可以先一圈一圈的打印。先打印外圈，再缩小边界范围循环打印内圈即可。打印的时候注意控制边界。

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public class 顺时针打印二维数组 {

	public static void main(String[] args) {
		int[][] matrix = {{1, 2, 3, 4},
						  {5, 6, 7, 8},
						  {9, 10, 11, 12},
						  {13, 14, 15, 16}};
		print(matrix);
	}

	public static void print(int[][] matrix) {
		
		int leftUpRow = 0, leftUpCol = 0;
		int rightDownRow = matrix.length - 1;
		int rightDownCol = matrix[0].length - 1;
		while(leftUpCol <= rightDownCol && leftUpRow <= rightDownRow) {
			int c = leftUpCol, r = leftUpRow;
			// 打印上面一条边
			while (c <= rightDownCol) {
				System.out.print(matrix[r][c++] + " ");
			}
			// 恢复
			c = rightDownCol;
			r++;
			//打印右边一条边
			while (r <= rightDownRow) {
				System.out.print(matrix[r++][c] + " ");
			}
			// 恢复
			r = rightDownRow;
			c--;
			//打印下面一条边
			while (c >= leftUpRow) {
				System.out.print(matrix[r][c--] + " ");
			}
			// 恢复
			c = leftUpRow;
			r--;
			//打印下面一条边
			while (r > leftUpRow) {
				System.out.print(matrix[r--][c] + " ");
			}
			leftUpCol++;leftUpRow++;rightDownCol--;rightDownRow--;
		}
	}
}

程序运行结果：

1
1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10

0所在的行列清零：

题目：

如果矩阵中某个元素为0，则将其所在的行和列清零。

1 2 3 4

5 6 0 8

9 0 11 12

13 14 15 16

思路：

先扫描整个二维数组，开辟两个一维数组，分别标记零所在的行和列。最后，在整个二维数组中，如果发现行或者列被标记，所在的行或者列的数据就清零。

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class 零所在的行和列清零 {

	public static void main(String[] args) {
		int[][] matrix = {{1, 2, 3, 4},
						{5, 0, 7, 8},
						{9, 10, 0, 12},
						{13, 14, 15, 16}};
		clear(matrix);
		util.ArrayUtil.printMatrix(matrix);
		
	}

	public static void clear(int[][] matrix) {
		// 标记0所在的行
		int[] rowFlag = new int[matrix.length];
		// 标记0所在列
		int[] colFlag = new int[matrix[0].length];
		for(int i = 0; i < matrix.length; i++) {
			for(int j = 0; j < matrix[0].length; j++) {
				if(matrix[i][j] == 0) {
					rowFlag[i] = 1;
					colFlag[j] = 1;
				}
			}
		}
		
		for(int i = 0; i < matrix.length; i++) {
			for(int j = 0; j < matrix[0].length; j++) {
				// 如果行或者列被标记，则该行和该列的所有数据清零
				if(rowFlag[i] == 1 || colFlag[j] == 1) {
					matrix[i][j] = 0;
				}
			}
		}
	}
}

程序运行结果：

1
2
3
4
1	0	0	4	
0	0	0	0	
0	0	0	0	
13	0	0	16

Z字形打印矩阵：

题目：

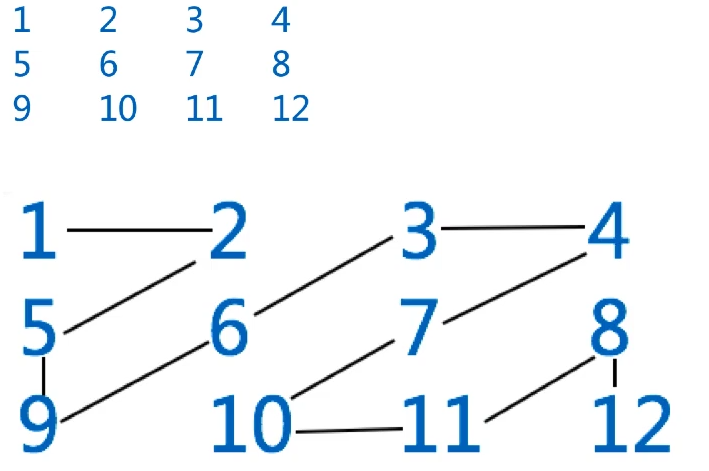
按如下规律，打印出矩阵元素。

Z形打印

思路：

做该题时，可以分解为打印两个方向，从左下角打印到右上角，再从右上角打印到左下角。分别控制好边界的转化方向即可。

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
public class Z形打印矩阵 {

	public static void main(String[] args) {
		int[][] matrix = {{1, 2, 3, 4},
				  		{5, 6, 7, 8},
				  		{9, 10, 11, 12}};
		zPrint(matrix);
	}

	public static void zPrint(int[][] matrix) {
		int row = matrix.length;
		int col = matrix[0].length;
		int r = 0;
		int c = 0;
		// 打印方向，true为从左下角向右上方打印。false为从右上方像向左下方打印
		boolean direction = true;
		while(r < row && c < col) {
			if(direction) {
				// 从左下到右上的斜线
				System.out.print(matrix[r][c] + " ");
				// 在第一行，列未到边界，只能向右走
				if(r == 0 && c < col - 1) {
					c++;
					direction = false;
					continue;
				}else if(r > 0 && c == col - 1){//走到最后一列，只能向下走
					r++;
					direction = false;
					continue;
				}else { // 继续走上坡
					r--;
					c++;
				}
			}else { // 从右上角往左下角走
				System.out.print(matrix[r][c] + " ");
				// 走到第一列，行未到边界。只能往下走
				if(c == 0 && r < row - 1) {
					r++;
					direction = true;
					continue;
				}else if(r == row - 1){ // 走到最后一行，只能往右走
					direction = true;
					c++;
					continue;
				}else { // 继续走下坡路
					r++;
					c--;
				}
			}

程序运行结果：

1
1 2 5 9 6 3 4 7 10 11 8 12

边界为1的最大子方阵：

题目：

给定一个N * N 的矩阵matrix，这个矩阵中，只有0和1两种值，返回边框全是1的最大正方形的边长长度。

例如：

1
2
3
4
5
6
> {0, 1, 1, 1, 1},
> {0, 1, 0, 0, 1},
> {0, 1, 0, 0, 1},
> {0, 1, 1, 1, 1},
> {1, 1, 0, 1, 1}	
>

其中，边框全是1的最大正方形的大小是4*4，返回4.

思路：

本题为基础解法，枚举。下道题该题的优化的解法。

枚举，从n ~ 1 遍历每个正方形的四条边，如果四条边都是1，则返回n。

代码示例:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
public class 边界为1的最大子方阵 {

	public static void main(String[] args) {
		int[][] matrix = {
				{0, 1, 1, 1, 1},
				{0, 1, 0, 0, 1},
				{0, 1, 0, 0, 1},
				{0, 1, 1, 1, 1},
				{1, 1, 0, 1, 1}};
		int max = solve(matrix);
		System.out.println(max);
	}

	private static int solve(int[][] matrix) {
		int N = matrix.length; 
		int n =N; //记录最大子方阵边长
		while (n > 0) { 
			for(int i = 0; i < N; i++) {
				if(i + n > N) break; 
				L3: // 标签，当在检查子方阵边长时，如果遇到边长有0，则跳出循环，重新继续执行下一行
				for(int j = 0; j < N; j++) {
					if(j + n > N) break;
					//检查四条边是否全为1
					int row = i;
					int col = j;
					//判断上边一条边
					while (col < j + n) {
						if(matrix[row][col++] == 0) {
							continue L3;
						}
					}
					col--;
					//判断右边一条边
					while (row < i + n) {
						if(matrix[row++][col] == 0) {
							continue L3;
						}
					}
					row--;
					//判断下边一条边
					while (col >= j) {
						if(matrix[row][col--] == 0) {
							continue L3;
						}
					}
					col++;
					//判断左边一条边
					while (row >= i) {
						if(matrix[row--][col] == 0) {
							continue L3;
						}
					}
					return n;
				}
			}
			n--;
		}
		return 0;
	}

}

程序运行结果：

1
4

边界为1的最大子方阵优化：

思路分析：

上题中的枚举算法时间复杂度为O(n^4), N N N * 4n的时间复杂度。

可以通过优化4n的时间复杂度，将整个解法的时间复杂度降到O(n^3).

思路：预处理方法。

​ 通过预处理方法，先生成一个对应的三维数组，二维平面空间和矩阵大小相等，第三维存储两个元素，第一个数表示，包括自己以及右方连续为1的个数，如果自己为0，则该数为0。第二个数表示，包括自己以及下方连续为1的个数，如果自己为0，则该数为0。通过生成这个辅助表，可以在判断是否是最大方阵的时候大大加快判断速度，可将4个while循环去除，每次只需判断一次即可，判断复杂度变为O(1)。

生成辅助举证举例如下：矩阵为记为A

1
2
3
4
5
6
> {0, 1, 1, 1, 1},
> {0, 1, 0, 0, 1},
> {0, 1, 0, 0, 1},
> {0, 1, 1, 1, 1},
> {1, 1, 0, 1, 1}	
>

如以上矩阵可以生成如下辅助数组help：

1
2
3
4
5
6
7
8
> {{0， 0}, {4， 4}, {3, 1}, {2, 1}, {1, 5}},
> {{0， 0}, {1， 4}, {0, 0}, {0, 0}, {1, 4}},
> {{0， 0}, {1， 3}, {0, 0}, {0, 0}, {1, 3}},
> {{0， 0}, {4, 2}, {3, 1}, {2, 2}, {1, 2}},
> {{2， 1}, {1， 1}, {0, 0}, {2, 1}, {1, 1}}
> //注意：生成辅助数组时，因为每个点记录的都是右下方的统计值，所以
> //     必须从右下方开始倒退生成整个辅助数组。
>

当生成如上辅助数组时，每次检查四条边的时候，可以直接检查三个顶点的数字，即可判断是否四条边都是1。例如：当检查n=4时，检查到 A[0][1] 点时，可以直接判断（help[0][1][0] >= n &&help[0][1][1] >= n help[0][1+n][1] >= n help[0+n][1][0] >= n）如果都成立，即可知四条边上的值为1。此时直接返回n即可。具体代码示例如下：

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
public class 边界为1的最大子方阵_优化 {
	
	static int[][][] help; //声明全局变量，辅助数组
	public static void main(String[] args) {
		int[][] matrix = {
				{0, 1, 1, 1, 1},
				{0, 1, 0, 0, 1},
				{0, 1, 0, 0, 1},
				{0, 1, 1, 1, 1},
				{1, 1, 0, 1, 1}};
		generateHelp(matrix);
		System.out.println("生成的辅助数组数据如下：");
		System.out.println("-------------------------------------");
		printHelp(help, matrix.length);
		System.out.println("-------------------------------------");
		int max = solve(matrix);
		System.out.println("最大子方阵的边长为：" + max);
	}

	// 打印生成辅助的数组数据
	private static void printHelp(int[][][] help, int N) {
		for(int i = 0; i < N; i++) {
			for(int j = 0; j < N; j++) {
				System.out.print(help[i][j][0] + "," + help[i][j][1] + "\t");
			}
			System.out.println();
		}
	}

	// 生成辅助数组的方法
	private static void generateHelp(int[][] matrix) {
		int N = matrix.length;
		help = new int[N][N][2];
		int lastRow = N - 1; 
		// 先初始化最后一行辅助数据。用于生成其他数据
		for(int i = N - 1; i >= 0; i--) {
			int value = matrix[lastRow][i];
			if(value == 1) {
				if(i == N - 1) {
					// 当初始化最后一列时，如果value为1，则右边为1
					help[lastRow][i][0] = 1;
				}else {
					// 如果非最后一列，则右边的初始化为：从自身到右边的连续1的个数
					help[lastRow][i][0] = help[lastRow][i + 1][0] + 1;
				}
				// 当value=1时，下方1的个数初始化为1
				help[lastRow][i][1] = 1;
			}
		}
		// 生成整个辅助数组的数据
		for(int i = N - 2; i >= 0; i--) {
			for(int j = N - 1; j >= 0; j--) {
				int value = matrix[i][j];
				if(value == 1) {
					if(j == N - 1) {
						help[i][j][0] = 1;
					}else {
						// 当value=1时，右方连续1的个数
						help[i][j][0] = help[i][j+1][0] + 1;
					}
					// 当value=1时，下方连续1的个数
					help[i][j][1] = help[i+1][j][1] + 1;
				}
			}
		}
	}

	private static int solve(int[][] matrix) {
		int N = matrix.length; 
		int n =N; //记录最大子方阵边长
		while (n > 0) { 
			for(int i = 0; i < N; i++) {
				if(i + n > N) break; 
				for(int j = 0; j < N; j++) {
					if(j + n > N) break;
					if(check(i, j, n))
						return n;
				}
			}
			n--;
		}
		return 0;
	}

	//检查以matrix[i][j]为左顶点的，边长为n的方阵的边上的数是否都为1
	private static boolean check(int i, int j, int n) {
		// 左上角那个点往右数的1的数目要 >= n
		// 左上角那个点往下数的1的数目要 >= n
		// 右上角那个点往下数的1的数目要 >= n
		// 左下角那个点往右数的1的数目要 >= n
		if(help[i][j][0] >= n && help[i][j][1] >= n 
			&& help[i+n-1][j][0] >= n && help[i][j+n-1][1] >= n)
			return true;
		return false;
	}

}

程序运行结果：

1
2
3
4
5
6
7
8
9
生成的辅助数组数据如下：
-------------------------------------
0,0	4,5	3,1	2,1	1,5	
0,0	1,4	0,0	0,0	1,4	
0,0	1,3	0,0	0,0	1,3	
0,0	4,2	3,1	2,2	1,2	
2,1	1,1	0,0	2,1	1,1	
-------------------------------------
最大子方阵的边长为：4

子数组最大和累加：

题目：

给定一个数组arr，返回子数组的最大累加和。

例如：arr[1, -2, 3, 5, -2, 6, -1]；所有的子数组中[3, 5, -2, 6]可以累加出最大和12，所以返回12；

思路：

有两种解法：

  • 方法1 ： 暴力法

    可以通过暴力法，把所有可能的子数组情况进行累加。最后比较，得出最大值即可。

    时间复杂度为：O(n^2);

  • 方法2：递推法：

    可以通过扫描一次数组，挨着累加，当累加和出现负数，直接舍弃，证明该段子数量最最大子序列没有贡献。每次累加后，与最大的数比较，如果比最大数大，就替换。详细代码如下：

    时间复杂度为：O(n)

代码示例:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public class MaxSubArray {

	public static void main(String[] args) {
		//获取10000 个 -100 - 100 的随机整数
		int[] arr = util.ArrayUtil.getRandomArr(10000, -100, 100);
		util.ArrayUtil.printArr(arr);
		long begin = System.currentTimeMillis();
		System.out.println("子数组最大累加和为：" + maxSum(arr));
		System.out.print("暴力法：");
		util.CountTime.countTime(begin);
		long begin1 = System.currentTimeMillis();
		System.out.println("子数组最大累加和为：" + maxSum1(arr));
		System.out.print("递推法：");
		util.CountTime.countTime(begin1);

	}
	
	//暴力法
	public static int maxSum(int[] arr) {
        if(arr.length == 0) return 0;
		int maxSum = arr[0]; //用来记录最大的和
		for(int i = 0; i < arr.length; i++) {
			int sum = 0; 
			for(int j = i; j < arr.length; j++) {
				sum += arr[j];
				if(sum > maxSum) {
					maxSum = sum;
				}
			}
		}
		return maxSum;
	}

	// 递推法 时间复杂度O(n)
	public static int maxSum1(int[] arr) {
        if(arr.length == 0) return 0;
		int maxSum = arr[0];
		int sum = 0;
		// left，right用来记录最大子序列和的开始和结束下标
		int left = 0, right = 0;
		for(int i = 0; i < arr.length; i++) {
			if(sum >= 0) { //左子表的最大和为正，继续向后累加
				sum += arr[i];
			}else { //为负，则舍弃，从下一个数重新开始累加。
				sum = arr[i];
				left = i; //记录左开始累加的左下标
			}
			
			if(sum > maxSum) { //如果每次累加的和大于最大记录，则替换
				maxSum = sum;
				right = i; //替换后此时，记录最大子序列的右下标
			}
		}
		System.out.println("最大子序列和的开始下标和结束下标为：" + left + "->" + right);
		return maxSum;
	}
}

程序执行结果：

1
2
3
4
5
6
31 78 93 99 -64 78 41 35 …… 
子数组最大累加和为：4253
暴力法：程序执行时间：54ms
最大子序列和的开始下标和结束下标为：8995->3811
子数组最大累加和为：4253
递推法：程序执行时间：0ms

子矩阵最大累加和：

题目：

给定一个矩阵matrix，其中的值有正、有负、有0，返回子矩阵的最大累加和。

例如：matrix 为：

1
2
3
4
> -1 -1 -1
> -1  2  2
> -1 -1 -1
>

其中最大累加和的子矩阵为：2 2 ，所以返回4.

思路：

有两种方案：

  • 方案1：暴力法，求出所有可能性。不推荐。

  • 方案2：递推法，同上题。

    每行为单位，求出单行的最大子序列和。将多行的值累加为一行的值进行累加。最后求出最大值。

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
public class MaxSubMatrix {

	public static void main(String[] args) {
		int[][] matrix = {{-1, -1, -1},
						   {-1, 2, 2},
						   {-1, -1, -1}};
		System.out.println(maxSubMatrixSum(matrix));
	}

	private static int maxSubMatrixSum(int[][] matrix) {
		if(matrix.length == 0) return 0;
		final int row = matrix.length;
		final int col = matrix[0].length;
		int maxSum = 0; //历史最大的子矩阵和
		int beginRow = 0;//以它为起始行
		while(beginRow < row) {
			//按列求和
			int[] sums = new int[col]; 
			for(int i = beginRow; i < row; i++) {
				//按列累加
				for(int j = 0; j < col; j++) {
					sums[j] += matrix[i][j];
				}
				//累加完成 该方法头上题解法2
				int sum = maxSubArraySum(sums);
				if(sum > maxSum) {
					maxSum = sum;
				}
			}
			beginRow++;
		}
		return maxSum;
	}

	private static int maxSubArraySum(int[] arr) {
		if(arr.length == 0) return 0;
		int maxSum = arr[0];
		int sum = 0;
		for(int i = 0; i < arr.length; i++) {
			if(sum >= 0) { //左子表的最大和为正，继续向后累加
				sum += arr[i];
			}else { //为负，则舍弃，从下一个数重新开始累加。
				sum = arr[i];
			}
			
			if(sum > maxSum) { //如果每次累加的和大于最大记录，则替换
				maxSum = sum;
			}
		}
		return maxSum;
	}
}

程序运行结果：

1
4
坚持原创技术分享，您的支持将鼓励我继续创作！