快速排序扫描分区法:
通过单向扫描,双向扫描,以及三指针分区分别实现快速排序算法。着重体现分区的思想。
一遍单向扫描法:
思路:
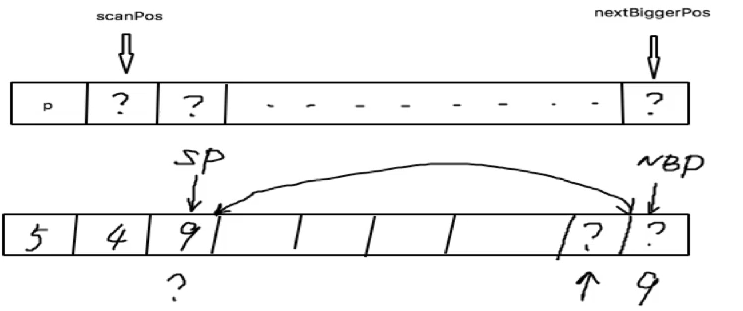
一遍扫描法的思路是,用两个指针将数组划分为三个区间,
扫描指针(scan_pos)左边是确认小于等于主元的,扫描指针到某个指针(next_bigger_pos)中间为未知的,因此我们将第二个指针(next_bigger_pos)成为位未知区间末指针,末指针的右边区间为确认大于主元的元素。
代码示例:
1 | public class QuickSrot { |
程序运行结果:
1 | 97 15 1 32 44 33 27 98 36 30 34 74 83 98 44 |
双向扫描分区法:
思路:
双向扫描的思路是,头尾指针往中间扫描,从左找到大于主元的元素,从右找到小于等于主元的元素二者交换,继续扫描,直到左侧无大于元素,右侧无小于主元元素。
代码示例:
1 | public class QuickSrot { |
程序运行结果:
1 | 53 4 87 32 24 99 18 74 91 56 52 24 38 76 30 |
三分法:
思路:
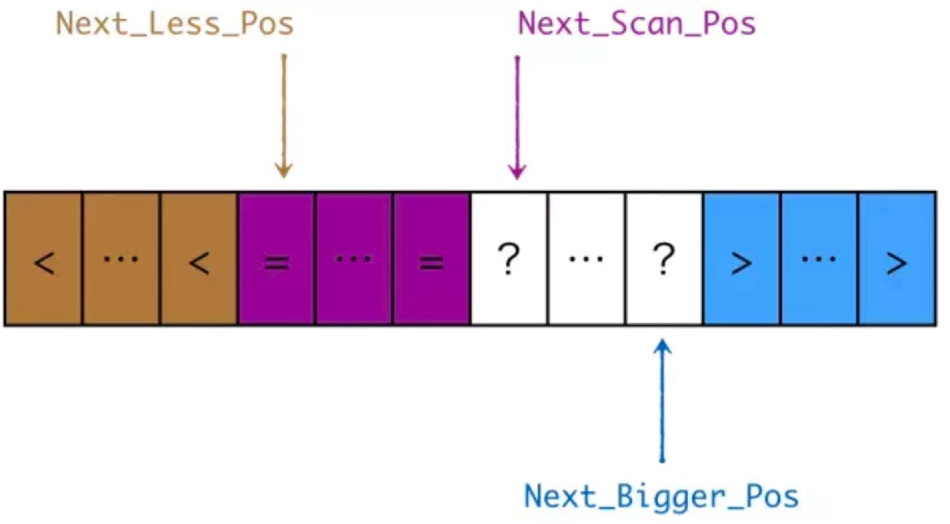
当待排序数组中,如果有大量相同的元素,则可用三分区法,每次将与主元相等的元素找到,排行序,并记录这组主主元相等元素序列的开始下标和结束下标。在进行下次递归排序是,排除这部分相同的元素。从而减少递归次数。
如上图,紫色部分为拍好序的与主元相等的元素,在递归拍其它两边的元素时,可排除这部分元素。具体实现代码如下:
代码示例:
1 | package chapter3_排序; |
程序运行结果:
1 | 5 5 1 8 8 5 6 3 8 2 6 1 6 3 0 |
快速排序优化_三点中值法:
思路:
上面三个例子中,每次取得主元都是待排序子序列的开始第一个元素,很大可能不是属于中间的元素,从而容易加大递归的层数。
通过三点中值法,对比待排序序列的开始,中间,最后三个元素的大小,去中间值,更大概率能使主元选择成为中间的元素,从而减少递归层数。
代码示例:
1 | package chapter3_排序; |
程序运行结果:
1 | 20 76 81 19 9 74 48 69 62 98 37 14 96 6 40 |
快速排序优化_绝对中值法:
思路:
三点中值法也有很大的随机性,如果想要得到绝对的中值,可以通过绝对中法来获取主元。通过将待排序序以5分为一组,去中间值,取到整个数组的各组中间值,再将这些数组排序,主元取中间值。
一般因为寻找绝对中值,也会花费时间。所以使用三点中值法居多
代码示例:
1 | package chapter3_排序; |
程序运行结果:
1 | 39 27 73 78 80 69 42 99 19 87 74 14 50 15 21 |
快速排序优化_待排序列较短时,用插入排序:
思想:
当待拍序列较短时,如果一直用递归,花费的时间远比,用插入排序长。所以当待拍序列小于一定长度时,可使用插入排序,提高速度。
代码示例:
1 | package chapter3_排序; |
程序运行结果:
1 | 86 2 79 72 34 2 20 50 44 75 97 86 93 64 3 5 67 72 22 56 37 69 55 55 53 |