题目:巧用进制,天平称重
用天平称重时,我们希望用尽可能少的砝码组和出尽可能多的重量。如果有无限个砝码,但他们的重量分别是1,3,9,27,81,······等3的指数幂。神奇之处在于用他们的组和可以称出任意整数重量(砝码允许放在左右两个盘子中)。
本题目要求编程实现:对用户给定的重量,给出砝码组和方案,重量<100000.
例如:用户输如:5
程序输出: 9 -3-1
解题思路:
利用进制来解。
因为1,3, 9······都是3的幂,所以用3进制来解。
例如:
2
3
4
5
6
7
8
9
10
11
> 答案为 9 -3 -1
> 对应三进制为 1 -1 -1
>
> 因为每个砝码只能用一次。所以将1, 2 进位
> 2 进位需要加1,所有进位在该为再减1,即 1 ,2 变为 2, -1
> 将2继续进位可变为: 1, -1 ,-1
>
> 此时对应的数正好可转为:1 * 3^2, -1 * 3^1 ,-1 * 3^0
> 即对应: 9 -3 -1 正好为答案。
>
java代码示例:
1 | import java.util.ArrayList; |
程序运行结果:
1 | 5 |
题目:Nim游戏
一共有N堆石子,编号1-n ,第i堆中有a[i]个石子。每一次操作Alice和Bob可以从任意一堆石子中取出任意数量的石子,至少取一颗,至多取出这一堆剩下的所有石子。
两人轮流行动,取光所有石子的一方获胜。Alice为先手。
给定a,假设两人都采取最优策略,谁会获胜。
解题思路:
利用二进制异或。
解题示例:
2
3
4
5
6
7
8
9
10
11
> 变为二进制位 3 0 1 1
> 4 1 0 0
> 异或 5 1 0 1
> --------------------------
> 0 1 0
> 每次当轮到自己时异或结果为0,对手采取最优策略则自己输。
> 如果轮到自己时,异或结果非0,则自己必胜。
>
> 每次拿取石子策略,留给对手的异或结果为0,则必胜
>
java代码示例:
1 | public class Nim游戏 { |
程序运行结果:
1 | true |
题目:识别Nim问题,Georgia and Bob
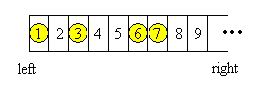
Georgia和Bob决定玩一个自己发明的游戏。他们在纸上画一排网格,从左到右给网格编号1、2、3、…,放置N个棋子或不同网格,如下图所示:
Georgia和Bob轮流移动棋子。每次玩家将选择一个棋子,并将其移动到左边,而不越过任何其他棋子或他的左边缘。掠夺者可以自由选择棋子移动的步数,约束条件是棋子必须移动至少一步,一个网格最多只能包含一个棋子。不会走一步棋的菜鸟输了这场比赛。
自从“女士优先”以来,Georgia总是第一个上场。假设Georgia和Bob都在游戏中表现最好,即如果他们中的一个人知道赢得比赛的方法,他或她就能实现它。即使是n个棋子的初始位置,你能预测出最终谁会赢吗
输入:
输入的第一行包含单个整数T (1 <= T <= 20),即测试用例的数量。然后T个例子。每个测试用例包含两行。第一行包含一个整数N (1 <=N <= 1000),表示棋子的数量。第二行包含N个不同的整数P1 P2。。Pn (1 <= Pi <= 10000),是n个棋子的初始位置。
输出:
输出对于每个测试用例,打印一行“Georgia will win”,如果Georgia愿意参与游戏;”Bob will win”,如果Bob会赢的话;否则“Not sure”
示例输入:
2
3
4
5
6
> 3
> 1 2 3
> 8
> 1 5 6 7 9 12 14 17
>
示例输出:
2
3
> Georgia will win
>
解题思想:
首先要识别出这是一个Nim问题。
以两个一组作为一堆。
java代码示例:
1 | import java.util.Arrays; |
程序运行结果:
1 | 2 |
欧几里得算法
1 | public class 欧几里得算法 { |