动态规划算法简介:动态规划算法
背包问题:
有n个重量和价值分别为wi,vi的物品,从这些物品中挑选出总重量不超过W的物品,求所有挑选方案中价值总和的最大值。
1≤n≤100 1≤wi,vi≤100 1≤W≤10000输入:
n=4 (w,v)={(2,3),(1,2),(3,4),(2,2)} W=5输出:
7(选择第0,1,3号物品)因为对每个物品只有选和不选两种情况,所以这个问题称为01背包。
Java代码示例:
1 | import java.util.Arrays; |
程序运行结果:
1 | 7 |
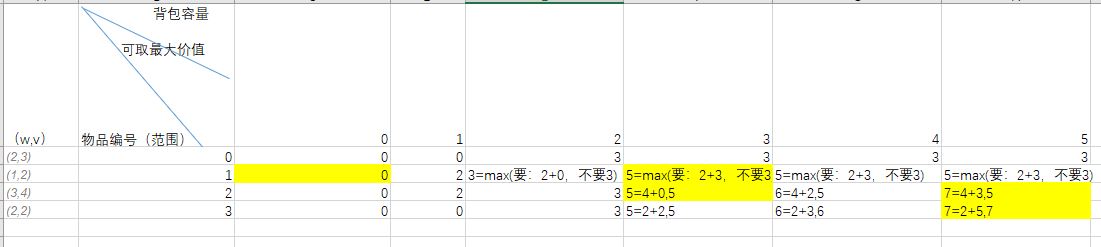
背包问题动态规划解法:
解题思路:
Java代码示例:
1 | public class 背包问题dp { |
程序运行结果:
1 | 7 |